本篇目录:
求解二阶电路
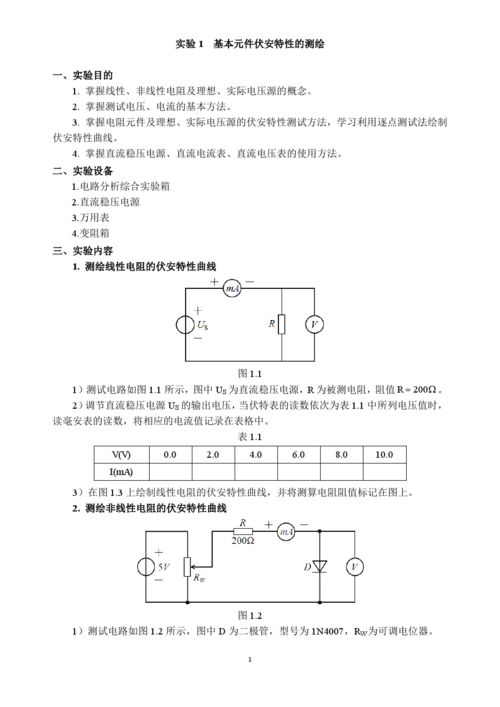
解:t=0-时,电容相当于开路,uc(0-)=3×50=150(V)。换路定理:uc(0+)=uc(0-)=150V。换路后,RLC二阶电路组成串联回路的零输入响应,其中:R=5kΩ,L=5H,C=625nF=25/10^7(F)。
看图,iL(0+)=-0.5A,uc(0+)=0.5V,uR(0+)=0.25V,duc(0+)/dt=0.25,diL(0+)/dt=1。解题思路:电容电压不跃变,电感电流不跃变,由此画出暂态电路,求出所有暂态值。
既然电流表读数不变,说明电路阻抗值不变,只是相角改变,且改变前后相角对称。
解:你先画一个电路图:两灯都不亮,则一定是断路。电压表有示数,说明电压表两个接线柱跟电源两极相连接,这部分导线没断,那么只有L1断路了。例L1与L2串联,电压表V1测L1电压,V2测L2电压。
请问什么是二阶电路,什么是零状态响应?
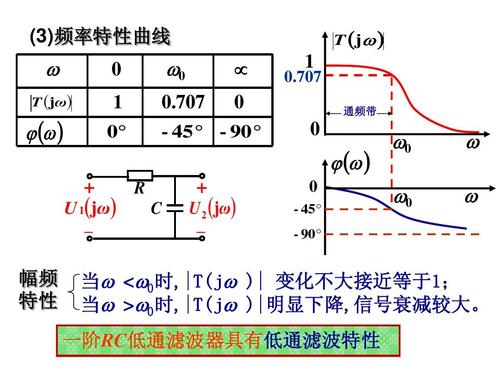
电路中含有一个独立的储能元件(电容或电感)的称为一阶电路。 若输入的激励信号为零,仅有储能元件的初始储能所激发的响应,称为零输入响应。 反之,电路的初始储能为零,仅由激励引起的响应为零状态响应。
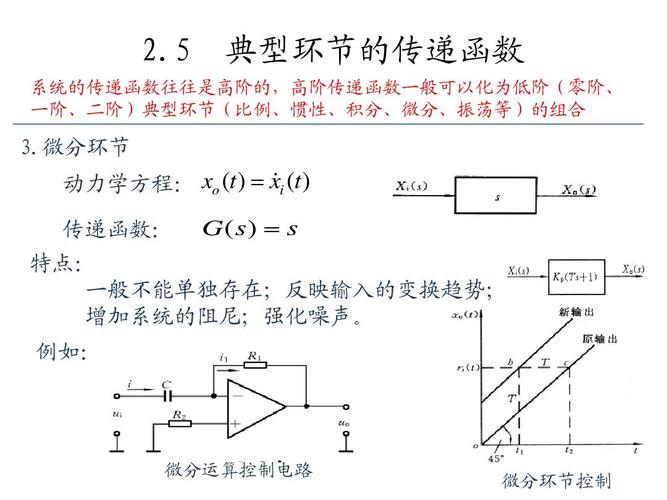
零状态响应 如果系统的初始状态为零,仅由激励源引起的响应就被称之为该系统的零状态响应。
二阶动态电路是含有两个独立的动态元件的线性电路,要用线性,常系数二阶微分方程来描述,故称为二阶动态电路。由电阻器、电感器和电容器串联或并联而成的电路是最简单的二阶动态电路。
电路中的响应是指激励在电路中各部分引起的电压和电流的输出,也称记忆函数。系统的响应除了激励所引起外,系统内部的“初始状态”也可以引起系统的响应。
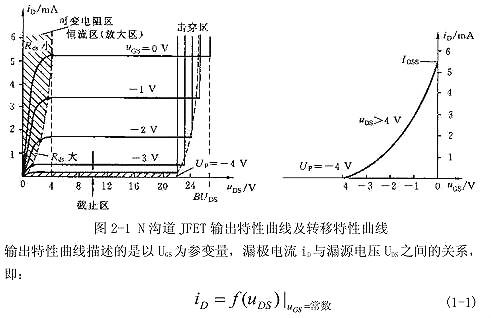
从电路来看,包含了L和C两个动态元件,应该是二阶电路。
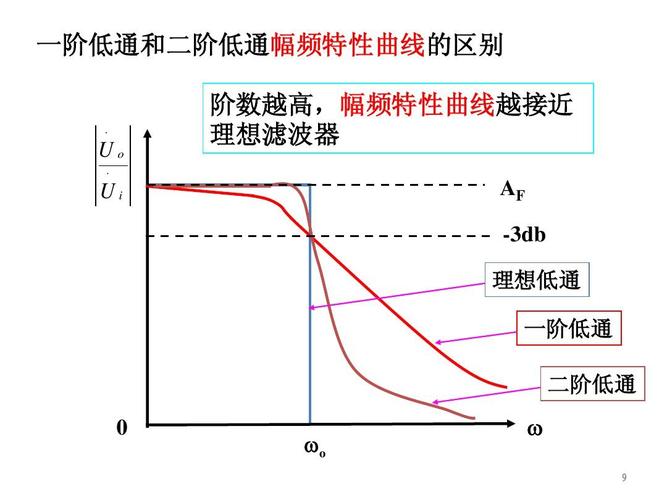
一阶电路和二阶电路的时域分析
1、一阶电路的特点是电路中的电容和电感会产生阻抗,同时电路中的电流和电压会随时间变化,因此一阶电路的时域分析是非常重要的。一阶电路的应用广泛,包括滤波器、振荡器、电流控制电路等。
2、第七章 一阶电路和二阶电路的时域分析第八章 相量法相量法(phaser method),分析正弦稳态电路的便捷方法。
3、记住 换路前后 电容电压不突变(q=cu)。电感电流不突变。
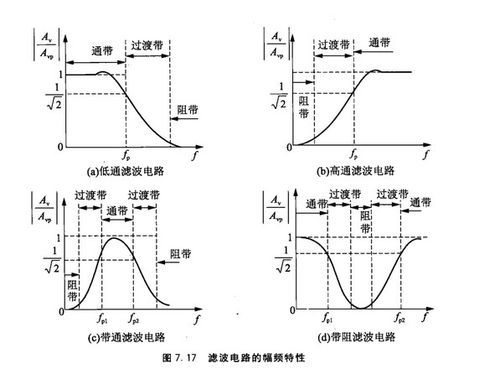
二阶有源滤波器电路的特性是什么?
压控二阶有源低通滤波器符合您描述的特点。二阶有源压控低通滤波器的传递函数为:Au(s)=Aup/(1+(3-Aup)sCR+(sCR)^2)当Aup=3时,传递函数有极点出现在复平面的右半平面,系统为不稳定系统。
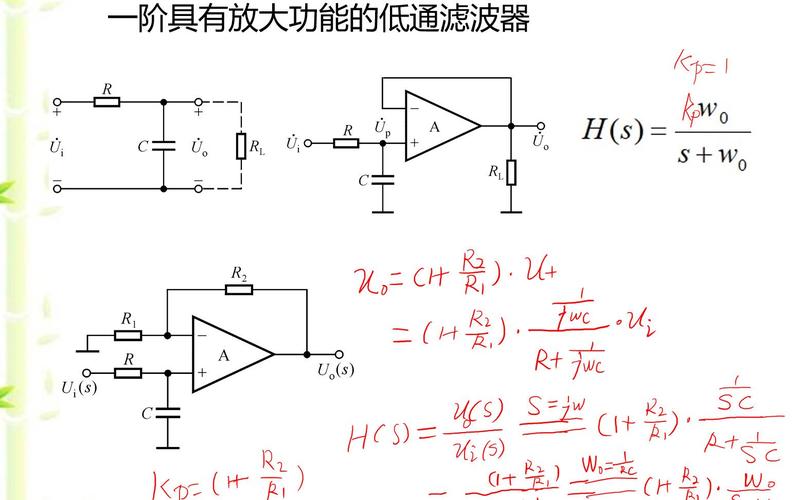
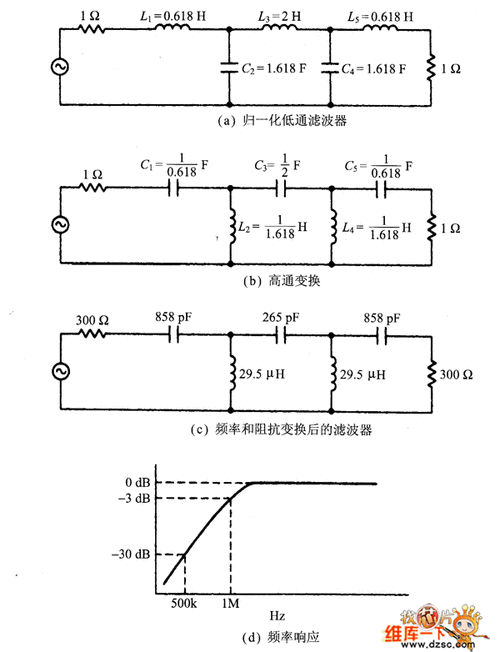
高阶滤波器通常可由一阶和二阶滤波器级联而成。采用集成运放构成的RC有源滤波器具有输入阻抗高,输出阻抗低,可提供一定增益,截止频率可调等特点 。
(1)二阶有源RC低通滤波器的幅频特性 图附录2—1 图附录2—1所示电路为二阶有源RC低通滤波器,运算放大器A构成同相放大器,其闭环增益为, (利用这一点可以判断运算放大器工作是否正常)。
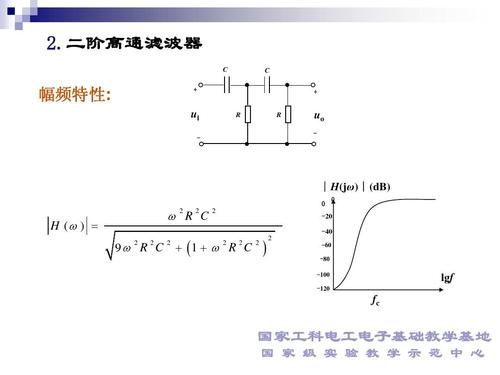
与低通滤波器相反,高通滤波器用来通过高频信号,衰减或抑制低频信号。只要将图2-2低通滤波电路中起滤波作用的电阻、电容互换,即可变成二阶有源高通滤波器,如图2-3(a)所示。
大学电路,二阶电路分析?
1、解:t=0-时,电容相当于开路,uc(0-)=3×50=150(V)。换路定理:uc(0+)=uc(0-)=150V。换路后,RLC二阶电路组成串联回路的零输入响应,其中:R=5kΩ,L=5H,C=625nF=25/10^7(F)。
2、看图,iL(0+)=-0.5A,uc(0+)=0.5V,uR(0+)=0.25V,duc(0+)/dt=0.25,diL(0+)/dt=1。解题思路:电容电压不跃变,电感电流不跃变,由此画出暂态电路,求出所有暂态值。
3、看图,i=(0.6+5t)e^-5t A。设电容电压为u,分别列出t0时,u和i的关系式以及KVL方程,联立得出变量为u的二阶微分方程,求出通解,代入初始条件,最后对u求导,i=0.08u。
4、二阶电路分类 零输入响应 系统的响应除了激励所引起外,系统内部的初始状态也可以引起系统的响应。
5、二阶电路三种阻尼状态图如下:含有两个独立的动态元件的线性电路,要用线性,常系数二阶微分方程来描述,故称为二阶电路。系统的响应除了激励所引起外,系统内部的“初始状态”也可以引起系统的响应。
6、一阶电路里有一个电容 或 一个电感。二阶电路里有一个电容和一个电感。简单的讲,一阶电路里有一个储能元件,可以是电容也可以是电感。
求这个二阶电路分析怎么解
1、解:t=0-时,电容相当于开路,uc(0-)=3×50=150(V)。换路定理:uc(0+)=uc(0-)=150V。换路后,RLC二阶电路组成串联回路的零输入响应,其中:R=5kΩ,L=5H,C=625nF=25/10^7(F)。
2、看图,iL(0+)=-0.5A,uc(0+)=0.5V,uR(0+)=0.25V,duc(0+)/dt=0.25,diL(0+)/dt=1。解题思路:电容电压不跃变,电感电流不跃变,由此画出暂态电路,求出所有暂态值。
3、看图,i=(0.6+5t)e^-5t A。设电容电压为u,分别列出t0时,u和i的关系式以及KVL方程,联立得出变量为u的二阶微分方程,求出通解,代入初始条件,最后对u求导,i=0.08u。
到此,以上就是小编对于二阶电路传输特性实验结果与讨论的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏