本篇目录:
什么叫ABCD光学系统
1、凹面镜的成像规律与凸透镜相似,焦点之内成正立、放大的虚像,不同的是成虚像时,物、像位于它的异侧。
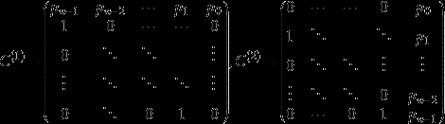
2、A为系统矩阵,B为控制矩阵,C为输出矩阵或观测矩阵,D为直接传递矩阵。状态方程是系统在时域的表达式,对于无理系统,往往是通过建模,推导和线性化得到的。

3、则可以看出a是一个上升的过程。那么冷空气来时,就是冷锋过境时就会气压上升。b是中间一个下凹,则说明是一个暖气团先占据了冷气团原来的位置,然后又离开依旧是冷气团控制。C是一个气压下降的过程。
这三道矩阵题怎么做
所以假设a[i]按从小到大顺序排列,则必有,a[i+1]=a[i]+1;所以a[n]-a[m]=n-m;由此得证。没有,若有,责说明任意两个n阶方阵乘积可交换,这是不可能的,很容易举出乘积不可交换的矩阵的反例。
矩阵C的第i行第j列的元素Cij就是取A的第i行元素、B的第j列元素,然后对应相乘。举个实际的例子来理解一下,比如下图所示的矩阵乘法。C11是由A的第一行与B的第一列对应相乘得到的,即C11=1×3+2×1+4×2=13。
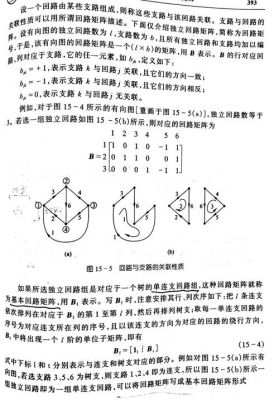
利用系数矩阵的秩,等于增广矩阵的秩,有解。
已知A矩阵,求A逆矩阵。可以使用初等变换来求解。初等变换有行初等变换和列初等变换两种。行(列)初等变换是通过每行(列)的加、减、乘、除的运算,将 A|E 转换成 E|A^(-1)。
二端口网络的说明
1、二端口网络的四种参数主要是阻抗参数Z;导纳参数Y;混合参数H;传输参数T。二端口网络,首先得保证有四个端口,而且两两相同。二端口网络是线性的,由电阻、电感(包括耦合电感)、电容、线性受控源组成。

2、二端口网络(英语:two-port network)又称双端口网络、双口网络,是四端子网络(四端网络)的一种,是具有2个端口的电路或装置,端口与电路内部网络相连接。
3、当确定端口1是入口、端口2是出口后,Y12是反向转移导纳,Y21是正向转移导纳。用类似的方法,可对其他参数作出相应的解释。 6组参数都可用来表征二端口网络。 对于一个网络究竟选用哪一组,视具体情况而定。
4、一端口网络的意思就是:(1)具有两个端的网络。(2)具有多于两个端,但所关注的只是其中两个端(作为一个端口)性能的网络。戴维南定理中介绍的二端网络为一端口网络。显然一端口网络两个端钮上的电流大小相等,方向相反。
5、结构简单:二端口网络只需两个端口,即输入端口和输出端口,设备之间相对独立,可以同时支持多个设备与主机的连接。
6、双口网络的外部特性,即端口上电压、电流之间的关系,可以用有两个方程的方程组来表示。由于可以用IUII2中的任意两个量来表示另外两个,所以有 多种组合,表1列出了常用的五种双口网络方程。
abcd四个三维向量组成一个向量组,一定线性相关吗?为什么?
1、设a1,a2,a3,a4是四个三维的向量组成的向量组,则此向量组必线性?为什么?这个有多种证明方法。将它们组成一个矩阵4*3,它的秩必然小于等于3,而有四行,则必然线性相关。
2、你好!有个定理:向量个数大于维数时一定线性相关。((a1,a2,a3,a4)的秩不会超过行数3,所以秩小于列数4)。经济数学团队帮你解请及时采纳。
3、判断向量组线性相关性的方法:写成矩阵形式,然后通过行变换,化为行最简形,得到矩阵的秩;得出矩阵的秩,用来和向量个数比较;因为向量组组成的矩阵的秩小于向量个数,所以得出。
4、这样来讲的话,包含n+1个向量的线性相关组,期中的这n+1个向量处于n维空间的这种情况反而是特殊情况。向量组线性相关的几何意义 两个2维向量a,b构成的向量组的几何意义是: a,b共线。
5、假设这四个向量线性无关,那么任取其中三个也是线性无关的,因为是三元数组,所以这三个向量可看作一个基,因此,第四个非零向量就可以由这一组基来线性表达并且系数不全为0,这与假设相矛盾,因此这四个向量线性相关。
矩阵与矩阵变换
变换是指我们把一些数据,顶点、方向矢量甚至是颜色等,通过某种方式进行转换的过程。
对矩阵作如下变换:换行变换:交换两行(列)。倍法变换:将行列式的某一行(列)的所有元素同乘以数k。消法变换:把行列式的某一行(列)的所有元素乘以一个数k并加到另一行(列)的对应元素上。
矩阵行列变换规则如下:矩阵的行和列:一个矩阵由行和列组成,通常表示为 m x n 的形式,其中 m 表示矩阵的行数,n 表示列数。例如,一个 3 x 2 的矩阵有3行和2列。
到此,以上就是小编对于传输线的abcd矩阵参数求解的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏