本篇目录:
传输函数和传递函数的区别
1、传递函数的表示方法:传递函数通常表示为一个复数函数,其中输入和输出分别表示为复数变量。传递函数通常具有以下形式:G(s) = Y(s)/U(s)其中,G(s)表示传递函数,Y(s)表示输出,U(s)表示输入,s为复数变量。
2、在工程中,传递函数(也称系统函数、转移函数或网络函数,画出的曲线叫做传递曲线)是用来拟合或描述黑箱模型(系统)的输入与输出之间关系的数学表示。
3、在控制系统中,传递函数是表示输入和输出之间关系的数学表达式,它是控制系统设计和分析的基础。传递函数可以通过多种方法求解,下面我将介绍一些常用的方法。
4、,传递函数是指零初始条件下线性系统响应(即输出)量的拉普拉斯变换(或z变换)与激励(即输入)量的拉普拉斯变换之比。
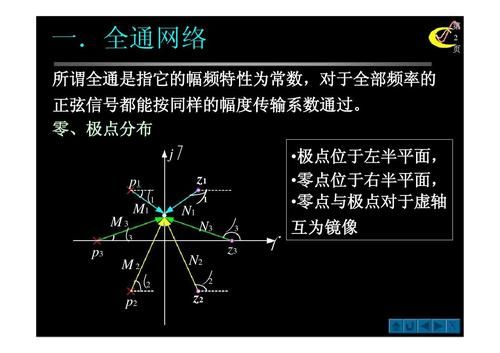
全通滤波器传递函数怎么计算?
1、通过公式计算G(s)=(G0*Wc)/(s+Wc)。所谓传递函数即线性定常系统在零初始条件下,输出量的拉氏变换式与输入量的拉氏变换式之比。

2、阶跃信号的Z变换可以很容易计算得到,为1/(1-z-1)。很显然,这个系统只有一个零点,其值为z=0;有一个极点,其值为z=1。
3、将输入信号表示为复频域中的函数(一般为s域),用复频率s代替常规频频jω。将电路中的程序转换为传讯号码格式,即输入号码与输入号码的比值。
4、额 通过传递函数我们就可以确定滤波器的通性情况。DSP中传递函数一般都是给的Z变换形式。我们可以通过求其幅频特性来观察出通性。
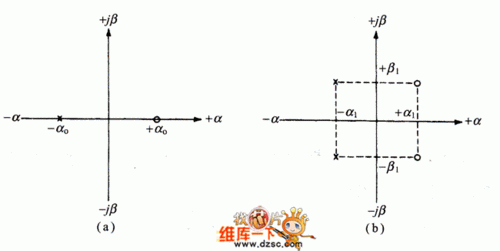
5、计算极点的频率。根据通带截止频率和阻带截止频率,计算出滤波器的极点频率。计算极点的品质因数。根据通带最大衰减和阻带最小衰减,计算出滤波器的极点品质因数。计算传递函数。
四种网络的幅频特性的特点
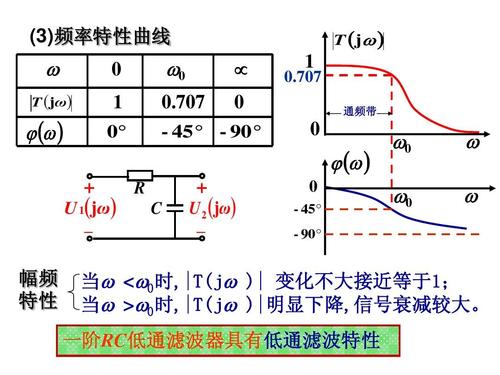
1、以下是对四种常见网络的幅频特性特点的描述: 低通滤波器:低通滤波器的传输函数在低频处具有较高增益,而在高频处具有较低增益。因此,低通滤波器可以通过滤除高频信号,从而只保留低频信号。
2、扫频法;连续冲击脉冲生成,求其冲激响应得到的幅频包络线;点频法;与扫频法类似,只是离散频点进行冲击计算;相频特征是滞后角与频率之间的关系,是强迫振动的相对误差,也就是动态与静态响应时间误差。
3、G(jω)称为频率特性,A(ω)是输出信号的幅值与输入信号幅值之比,称为幅频特性。Φ(ω)是输出信号的相角与输入信号的相角之差,称为相频特性。相移角度随频率变化的特性叫相频特性。
到此,以上就是小编对于简述全通系统及全通函数的定义的问题就介绍到这了,希望介绍的几点解答对大家有用,有任何问题和不懂的,欢迎各位老师在评论区讨论,给我留言。

 微信扫一扫打赏
微信扫一扫打赏