传输函数逆z变换（传递函数的逆过程怎么求）-共工科技

本篇目录：

传递函数是一种数学模型，与系统的微分方程相对应。是系统本身的一种属性，与输入量的大小和性质无关。只适用于线性定常系统。传递函数是单变量系统描述，外部描述。

传递函数的性质如下：１．传递函数是描述线性系统或线性元件特性的一种数学模型，它和系统或元件的运动微分方程一一对应。２．传递函数反映系统本身的瞬态特性。它只与系统本身结构参数有关。３．传递函数不反映系统的物理结构。

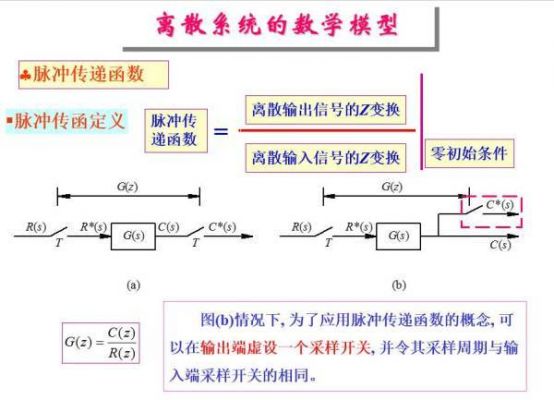
传递函数的性质传递函数仅描述系统在零初始条件下输入和输出之间的关系，不反映系统内部中间变量如何传递。它在离散时间信号处理中的地位，如同拉普拉斯变换在连续时间信号处理中的地位。

传递函数是描述输入信号和输出信号之间的关系的函数。它通常用于描述线性时不变系统的动态性质。

1、1通信与信息系统、081002信号与信息处理：电路与数字信号处理：《电路》（第四版）邱关源，高等教育出版社；或《电路分析基础》（第三版）李瀚逊，高等教育出版社。

2、武汉大学计算机考研科目有思想政治理论、英语数学计算机基础、数据库原理。

3、杭州电子科技大学考研，通院的信号与信息处理考数学一和英语一。专业课是841数字信号处理或842通信原理或848信号系统与信号处理。自己网上报名时任意选择一科即可。

z变换和拉普拉斯变换的关系如下：拉普拉斯变换是傅立叶变换的推广，傅立叶变换不适用于指数级增长的函数，而拉氏变换相当于是带有一个指数收敛因子的傅立叶变换，把频域推广到复频域，能分析的信号更广。

拉普拉斯变换是傅立叶变换的推广，傅立叶变换不适用于指数级增长的函数，而拉氏变换相当于是带有一个指数收敛因子的傅立叶变换，把频域推广到复频域，能分析的信号更广。

Z变换它的极径=1，也就是单位圆周上的变换，本质上就还是傅里叶变换，Z与拉普拉斯的关系自然就是Z=e^st。总结如下：fourier变换是将连续的时间域信号转变到频率域；它可以说是laplace变换的特例。

对照采样序列的z变换：显然，当z=e^sT时，采样序列的z变换等于理想采样信号的拉氏变换。这说明，从理想采样信号的拉氏变换到采样序列的z变换，就是由复变量s平面到复变量z平面的映射变换，这个映射关系就是z=esT。

-06-11 简述傅里叶变换、拉普拉斯变换、Z变换三者之间的关系。

到此，以上就是小编对于传递函数的逆过程怎么求的问题就介绍到这了，希望介绍的几点解答对大家有用，有任何问题和不懂的，欢迎各位老师在评论区讨论，给我留言。